SWITCHES_example

Using the SWITCHES database

This example does the following:

1. Downloads a bistable model from the SWITCHES database.
2. Describes how a model is written in SWITCHES format.
3. Describes how bistable parameters are extracted for the database using Latin Hypercube Sampling and by finding steady-states using MOOSE.
4. Demonstrates deterministic and stochastic time-course simulation in MOOSE to visualize bistability.
In [1]:
import warnings
warnings.filterwarnings("ignore")
warnings.simplefilter("ignore")

import requests
import moose
import matplotlib
%matplotlib notebook
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from string import ascii_lowercase as al
import numpy as np
import lhsmdu

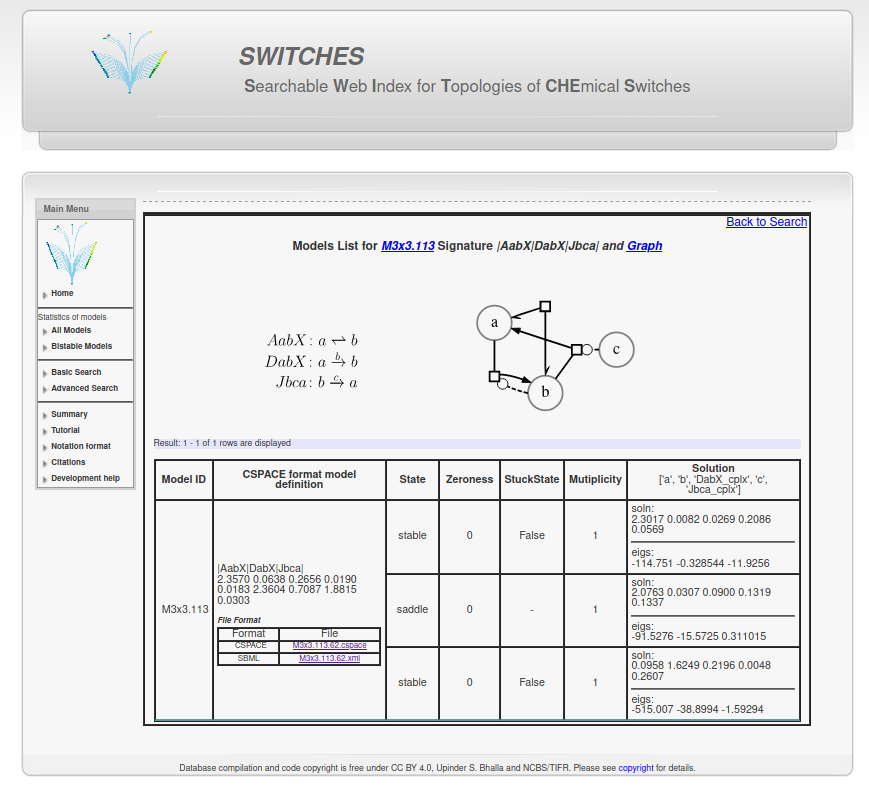
1. Downloading a CSPACE file from the SWITCHES database

1.1 Click on the "Bistable Models" in the left menu bar from the website homepage at http://switches.ncbs.res.in.

bistable_select.png

1.2 Select a model configuration size. In this example, we select 3x3 i.e. 3 reactions between 3 reactants.

3x3.png

1.3 Select a Model ID from this list. Here we pick M3x3.113.

ADJ.png

1.4 You can also search by configuration size or other parameters using the basic and advanced search functionality on the left menu bar.

basicSearch.png

1.5 Save the CSPACE (or SBML) file for further use.

This page displays the model structure on top with selected bistable model parameters and solutions. On top, you can see the chemical reaction on the left with corresponding chemical reaction network in the SBGN format on the right.

getCspace.png

1.6 Alternatively, get the CSPACE file directly from Python

In [2]:
url = 'https://switches.ncbs.res.in/file/M3x3.113.62.cspace'
r = requests.get(url, allow_redirects=True)
open('M3x3.113.62.cspace', 'wb').write(r.content)
In [3]:
modelName = "M3x3.113.62.cspace"

2. SWITCHES format

In [4]:
def parseTopology(model):
    readModel = open(model,'r')
    modelData = readModel.readlines()
    elements = modelData[0].split(' ')
    modelName, modelString, reactionPars = elements[0][:-1], elements[1], elements[2:]
    return modelName, modelString, reactionPars
In [5]:
def findNumReacs(modelString, reactionPars):
    ''' Finds the number of molecules and reactions in the topology '''
    reactionList = modelString.split('|')
    reactionDim = len(reactionList)-2 ## To get rid of the first and the last empty list and each reaction has 2 rates
    return reactionDim

2.1 SWITCHES format is a compact representation of a chemical reaction network.

It has three parts, model ID, model string, and the reaction parameters.

In [6]:
modelID, modelString, reactionPars = parseTopology(modelName)
In [7]:
print(modelID)

M3x3.113.62

2.2 Model ID is a hierarchical description of the model.

Level 1: M3x3 : Describes that the model has 3 reactants and 3 reactions respectively.

Level 2: 113 : Uniquely identifies the model string or the reaction network without the parameters.

Level 3: 62 : Uniquely identifies the reaction parameters of this reaction network.

In [8]:
print(modelString)

|AabX|DabX|Jbca|

2.3 Model string describes all the reactant and reactions in the reaction network.

model_image.png

The reactions are taken from this table of basic reaction types.

allReacs.png

The first letter (upper caps) describes the reaction type (A-L). The next three letters (lower caps) describe the reactant labels.

In [9]:
print(reactionPars)

['2.3570', '0.0638', '0.2656', '0.0190', '0.0183', '2.3604', '0.7087', '1.8815', '0.0303']

2.4 Reaction parameters are reactant concentrations and reaction constants (Kf, Kb for reversible and kcat and Km for enzymatic reactions).

First the concentration of reactants are ordered alphabetically. So, concentration of

$a = 2.3570 \mu M$ , $b = 0.0638 \mu M$ and $c = 0.2656 \mu M$.

Then for reversible, non-enzymatic reactions: Kf, Kb and for enzymatic reactions kcat, Km. Our model has two enzymatic reactions DabX and Jbca. Therefore, the order of reaction constants for this model is

$K_f(AabX): 0.0190 s^{-1}$ , $K_b(AabX) : 0.0183 s^{-1}$ , $k_{cat}(DabX): 2.3604 s^{-1}$ , $K_m(DabX): 0.7087 \mu M$ , $k_{cat}(Jbca): 1.8815 s^{-1}$ , $K_m(Jbca): 0.0303 \mu M$

3. Finding steady states with MOOSE

In [10]:
runtime = 500 #seconds
numIterations = 1000 # Number of times the steady-state finder will run with the same parameters.
numRates = 500 # Total number of random rates to sample
minScale = -1 # Minimum (Order of magnitude change in parameters)
maxScale = 1 # Maximum (Order of magnitude change in parameters)
microMolarScaling = 1e-3 # Scaling factor to convert to SI units of milliMolar
numMols = int(modelID[1]) # Number of reactants in the reaction network
numReacs = int(modelID[3])*2 # Two parameters for each reaction.
In [11]:
scalingVector = np.logspace(minScale, maxScale, num=numRates, base=10)

3.1 Simulating with MOOSE to find fixed points.

MOOSE steady state solver is used to find steady states of the reaction network for a random set of rates sampled above. The stability of these states is determined by analyzing the eigenvalues of the Jacobian around the fixed points found.

In [12]:
dj = moose.loadModel(modelName, 'model', 'gsl')
In [13]:
tolerance = 0.05 # parameters to determine when two concentration vectors can be called identical.
offset = 1e-3
In [14]:
def setupSteadyState(modelName, kineticsBasePath = '/model/kinetics'):    
    ''' Sets up steady-state finder in MOOSE'''
    simdt = 1e-3
    plotDt = 1e-2

    ksolve = moose.Ksolve( kineticsBasePath + '/ksolve' )
    stoich = moose.Stoich( kineticsBasePath +'/stoich' )
    stoich.compartment = moose.element(kineticsBasePath)
    stoich.ksolve = ksolve
    stoich.path = kineticsBasePath + "/##"
    state = moose.SteadyState( kineticsBasePath +'/state' )

    #### Set clocks here
    moose.useClock(4, kineticsBasePath +"/##[]", "process")
    moose.setClock(4, float(simdt))
    moose.setClock(5, float(simdt))
    moose.useClock(5, kineticsBasePath +'/ksolve', 'process' )
    moose.setClock(8, float(plotDt))

    moose.reinit()

    state.stoich = stoich
    state.convergenceCriterion = 1e-6
    
    return state, ksolve
In [15]:
def deleteSetup(kineticsBasePath = '/model/kinetics'):
    moose.delete(moose.Stoich(kineticsBasePath + '/stoich'))
    moose.delete(moose.Ksolve(kineticsBasePath + '/ksolve'))
    moose.delete(moose.SteadyState(kineticsBasePath + '/state'))
In [16]:
def uniqueElements(elements,errorRadius, offset):
    ''' Seperates out different numerically determined fixed points as identical or different'''
    uniqueList = []
    flag = 0
    finalList = []
#     multiplicity = []

    for element in elements:
        for iteration in range(len(uniqueList)):
            if len(uniqueList[iteration])>1:
                element2 = np.sum(uniqueList[iteration],0)/len(uniqueList[iteration]) ## Summing across an axis and averaging
            else:
                element2 = uniqueList[iteration][0]
            status = isSimilarTo(element, element2, errorRadius,offset)
            if (status):
                uniqueList[iteration].append(element)
                flag = 1
                break
            else:
                flag = 0
        if flag == 0:
            uniqueList.append([element])
  
    for iterable in uniqueList:
        elementAppend = np.sum(iterable,0)/len(iterable)
        finalList.append(elementAppend) 
#         multiplicity.append(len(iterable))
    return finalList
In [17]:
def isSimilarTo(list1, list2, tolerance, offset):
    ''' It takes in arrays and calculates element wise distances between them. The offset here can set the scale (for instance it is meaningless to detect less than a molcule'''
    distElementWise = [abs(a - b) for a,b in zip(list1,list2)]
    denominator = [a + b + offset for a,b in zip(list1,list2)] 
    diffError = [ (a/b) for a,b in zip(distElementWise,denominator)] ## upper bounded by 1 and lower bounded by zero.
    status = all(error <= tolerance for error in diffError)
    return status
In [18]:
def simpleaxis(axes, every=False):
    ''' Pretty plotting '''
    if not isinstance(axes, (list, np.ndarray)):
        axes = [axes]
    for ax in axes:
        ax.spines['top'].set_visible(False)
        ax.spines['right'].set_visible(False)
        if every:
            ax.spines['bottom'].set_visible(False)
            ax.spines['left'].set_visible(False)
        ax.get_xaxis().tick_bottom()
        ax.get_yaxis().tick_left()
        ax.set_title('')
In [19]:
a,b,c = [], [], []
kineticsBasePath = '/model/kinetics'

AabX = moose.element("/model/kinetics/AabX")
DabX = moose.element("/model/kinetics/b/DabX")
Jbca = moose.element("/model/kinetics/c/Jbca")

plota = moose.element("/model/graphs/plota")
plotb = moose.element("/model/graphs/plotb")
plotc = moose.element("/model/graphs/plotc")

state, ksolve = setupSteadyState(modelName)

original_AabX_Kf = AabX.Kf
original_AabX_Kb = AabX.Kb
original_DabX_Km = DabX.Km
original_Jbca_Km = Jbca.Km
original_DabX_kcat = DabX.kcat
original_Jbca_kcat = Jbca.kcat

3.2 First we find steady-states around a known set of bistable parameters to show how the model can gain or lose bistable behaviour.

In [20]:
AabX.Kf, AabX.Kb, DabX.Km, DabX.kcat, Jbca.Km, Jbca.kcat = [3.94276674e+00, 2.37393225e+02, 3.59605588e-01, 1.12050907e+02, 1.30874338e-03, 5.73402235e+01] # Known bistable parameters
DabX.Km*=microMolarScaling
Jbca.Km*=microMolarScaling

scaled_DabX_kcat = DabX.kcat * scalingVector

allStables_DabX = []
allUnstables_DabX = []
allSaddles_DabX = []

for scaled_kcat in scaled_DabX_kcat:
    stableVector = []
    unStableVector = []
    saddleVector = []
    
    DabX.kcat = scaled_kcat
    for iterations in range(numIterations):    
        deleteSetup()
        state, ksolve = setupSteadyState(modelName)
        state.randomInit()
#         moose.start(1)
        state.resettle()
        failedSteadyState = np.isnan(ksolve.nVec[0].any())
        if not failedSteadyState:
            vector = [pool.conc/microMolarScaling for pool in moose.wildcardFind(kineticsBasePath + '/##[ISA=PoolBase]')]
        if np.count_nonzero(vector)>1 and state.solutionStatus == 0:
            if state.stateType==0:
                stableVector.append(vector)
            elif state.stateType == 1:
                unStableVector.append(vector)
            elif state.stateType == 2:
                saddleVector.append(vector)
            else:
                print("Somthing strange found")
        moose.reinit()

    stable = uniqueElements(stableVector, tolerance, offset)
    unstable = uniqueElements(unStableVector, tolerance, offset)
    saddle = uniqueElements(saddleVector, tolerance, offset)
    
    allStables_DabX.append(stable)
    allUnstables_DabX.append(unstable)
    allSaddles_DabX.append(saddle)
In [21]:
isBistable = []
stable_a_high = []
stable_b_high = []
stable_a_low = []
stable_b_low = []
saddle_a = []
saddle_b = []
a_threshold, b_threshold = 2, 0.03

for j in range(numRates):
    stable = allStables_DabX[j]
    unstable = allUnstables_DabX[j]
    saddle = allSaddles_DabX[j]
    
    if len(stable) == 2:
        isBistable.append(1)
        
        stable_a_high.append(np.max(zip(*stable)[0]))
        stable_a_low.append(np.min(zip(*stable)[0]))
        stable_b_high.append(np.max(zip(*stable)[1]))
        stable_b_low.append(np.min(zip(*stable)[1]))

        if len(saddle):
            saddle_a.append(zip(*saddle)[0][0])
            saddle_b.append(zip(*saddle)[1][0])
        else:
            saddle_a.append(np.nan)
            saddle_b.append(np.nan)
    else:
        isBistable.append(0)
        
        ## Just to get pretty plots
        if np.max(zip(*stable)[0]) > a_threshold:
            stable_a_high.append(np.max(zip(*stable)[0]))
            stable_a_low.append(np.nan)
        else:
            stable_a_high.append(np.nan)
            stable_a_low.append(np.min(zip(*stable)[0]))
        
        if np.max(zip(*stable)[1]) > b_threshold:
            stable_b_high.append(np.max(zip(*stable)[1]))
            stable_b_low.append(np.nan)
        else:
            stable_b_high.append(np.nan)
            stable_b_low.append(np.min(zip(*stable)[1]))
        
        saddle_a.append(np.nan)
        saddle_b.append(np.nan)

3.3 1D bifurcation plot with DabX $k_{cat}$

Grey region shows the bistable area, where we found two stable fixed-points (grey dots) and saddle points (dotted black line).

In [22]:
oneIndices = np.arange(np.where(np.array(isBistable)==1)[0][0], np.where(np.array(isBistable)==1)[0][-1]+1)
bistableBoundaries = np.zeros(len(isBistable), dtype=int)
bistableBoundaries[oneIndices] = 1
In [23]:
# %matplotlib inline
fontsize = 12
fig, ax = plt.subplots()
ax.plot(scaled_DabX_kcat, stable_a_high,  c='grey')#, s=4)
ax.plot(scaled_DabX_kcat, stable_a_low,  c='grey')#, s=4)
ax.plot(scaled_DabX_kcat, saddle_a, 'k--')

ax.set_xlabel("DabX kcat ($s^{-1}$)", fontsize=fontsize)
ax.set_ylabel("Conc. a ($\mu$M)", fontsize=fontsize)
ax.set_xscale("log")
ax.set_xticks([10,100,1000])
ax.tick_params(axis='both', which='major', labelsize=fontsize)
ax.tick_params(axis='both', which='minor', labelsize=fontsize)

ax.fill_between(x=scaled_DabX_kcat, y1= ax.get_ylim()[0], y2 = ax.get_ylim()[1], where= list(bistableBoundaries), alpha=0.2, color='gray')
simpleaxis(ax)
fig.set_figwidth(5)
fig.set_figheight(5)
# plt.savefig("20915_BifurcationPlot_DabX.svg")
plt.show()
# plt.close()

3.3 Sampling efficiently across parameter space using latin hypercube sampling.

We use an efficient sampling method called Latin Hypercube sampling which allows us to sample high dimensionsal parameter space efficiently. The lhsmdu repo is available here https://github.com/sahilm89/lhsmdu.

In [24]:
minScale = -3 # Order of magnitude change in parameters
maxScale = 3
In [25]:
k = lhsmdu.sample(numReacs,numRates) ## Returns an efficient sample in numReacsxnumRates dimensions.
In [26]:
scalingVector = np.power(10,k*(maxScale-minScale) + minScale) ## Scaling logarithmically
In [27]:
scaled_AabX_Kf = np.array(scalingVector[0])[0]
scaled_AabX_Kb = np.array(scalingVector[1])[0]
scaled_DabX_Km = np.array(scalingVector[2])[0]
scaled_DabX_kcat = np.array(scalingVector[3])[0]
scaled_Jbca_Km = np.array(scalingVector[4])[0]
scaled_Jbca_kcat = np.array(scalingVector[5])[0]

rateMat = np.matrix([scaled_AabX_Kf, scaled_AabX_Kb, scaled_DabX_Km, scaled_DabX_kcat, scaled_Jbca_Km, scaled_Jbca_kcat])
In [28]:
rateNum = 0
allStables= []
allUnstables= []
allSaddles = []
for r in rateMat.T:
    aabx_kf, aabx_kb, dabx_Km, dabx_kcat, jbca_Km, jbca_kcat = np.ravel(r)

    stableVector = []
    unStableVector = []
    saddleVector = []
    
    AabX.Kf = aabx_kf
    AabX.Kb = aabx_kb
    DabX.Km = dabx_Km* microMolarScaling
    Jbca.Km = jbca_Km* microMolarScaling
    DabX.kcat = dabx_kcat
    Jbca.kcat = jbca_kcat
    
    deleteSetup()
    state, ksolve = setupSteadyState(modelName)
    
    for iterations in range(numIterations):    

        state.randomInit()

        state.resettle()
        failedSteadyState = np.isnan(ksolve.nVec[0].any())
        if not failedSteadyState:
            vector = [pool.conc/microMolarScaling for pool in moose.wildcardFind(kineticsBasePath + '/##[ISA=PoolBase]')]
        if np.count_nonzero(vector)>1 and state.solutionStatus == 0:
            if state.stateType==0:
                stableVector.append(vector)
            elif state.stateType == 1:
                unStableVector.append(vector)
            elif state.stateType == 2:
                saddleVector.append(vector)
            else:
#                 print("Strange ", state.stateType)
                pass
        moose.reinit()

    stable = uniqueElements(stableVector, tolerance, offset)
    unstable = uniqueElements(unStableVector, tolerance, offset)
    saddle = uniqueElements(saddleVector, tolerance, offset)
    
    allStables.append(stable)
    allUnstables.append(unstable)
    allSaddles.append(saddle)
    rateNum+=1
In [29]:
isBistable = []
stable_a_high = []
stable_b_high = []
stable_a_low = []
stable_b_low = []
saddle_a = []
saddle_b = []
for j in range(numRates):
    stable = allStables_DabX[j]
    unstable = allUnstables_DabX[j]
    saddle = allSaddles_DabX[j]
    
    if len(stable[0]) == 2:
        isBistable.append(1)
        saddle_a.append(zip(*saddle)[0][0])
        saddle_b.append(zip(*saddle)[1][0])
    else:
        isBistable.append(0)
        saddle_a.append(np.nan)
        saddle_b.append(np.nan)
    
    stable_a_high.append(np.max(zip(*stable)[0]))
    stable_a_low.append(np.min(zip(*stable)[0]))
    stable_b_high.append(np.max(zip(*stable)[1]))
    stable_b_low.append(np.min(zip(*stable)[1]))

3.4 2-D Bifurcation plot for two rates (DabX $k_{cat}$ and Jbca $k_{cat}$), but with all rates randomly sampled.

Black dots are bistable fixed points and orange dots are saddle points. Grey points are monostable.

In [48]:
%matplotlib inline
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
s = 48 #markersize
isBistable = []
#colors = plt.cm.viridis(np.linspace(0,1,numRates))
for j in range(numRates):
    stable = allStables[j]
    unstable = allUnstables[j]
    saddle = allSaddles[j]
    for fp in stable:
        if len(stable) ==2:
            ax.scatter(np.log10(scaled_DabX_kcat[j]), np.log10(scaled_Jbca_kcat[j]), fp[0],c='k', s=s, marker='.')
        else:
            ax.scatter(np.log10(scaled_DabX_kcat[j]), np.log10(scaled_Jbca_kcat[j]), fp[0],c='gray', s=s, marker='.')
    for fp in saddle:
        if len(stable[0]) ==2:
            ax.scatter(np.log10(scaled_DabX_kcat[j]), np.log10(scaled_Jbca_kcat[j]), fp[0], c='orange', s=s, marker='.')
        else:
            ax.scatter(np.log10(scaled_DabX_kcat[j]), np.log10(scaled_Jbca_kcat[j]), fp[0], c='orange', s=s, marker='.')
            
#     for fp in unstable:
#         ax.scatter(np.log10(scaled_DabX_kcat[j]), np.log10(scaled_Jbca_kcat[j]), fp[0], c='gray', s=24, marker='o')
        
    if len(stable) == 2:
        isBistable.append(1)
    else:
        isBistable.append(0)
    
ax.set_xlabel("DabX kcat ($s^{-1}$)", fontsize=fontsize)
ax.set_ylabel("Jbca kcat ($s^{-1}$)", fontsize=fontsize)
ax.set_zlabel("A (mM)", fontsize=fontsize)

ax.view_init(azim=44, elev=3)
ax.set_xticks([-3,0,3])
ax.set_yticks([-3,0,3])
ax.set_xticklabels(["$10^{-3}$","1","$10^{3}$"], fontsize=fontsize)
ax.set_yticklabels(["$10^{-3}$","1","$10^{3}$"], fontsize=fontsize)
fig.set_figwidth(5)
fig.set_figheight(5)
plt.show()

3.5 Rate-vector plot: The dark lines represent the bistable parameters among all the other (gray) parameter sets.

In [31]:
######### Here not plotting the parameter heatmap, but the line-plot. ##########
fig, ax = plt.subplots()

for i in range(rateMat.shape[1]):
    if isBistable[i] == 1:
        ax.plot(range(rateMat.shape[0]), np.ravel(rateMat[:,i]), c='k', alpha=1.0, linewidth=1, zorder=2)
    else:
        ax.plot(range(rateMat.shape[0]), np.ravel(rateMat[:,i]), c='gray', alpha=0.05, linewidth=1, zorder=1)
    
xticks = np.arange(0,rateMat.shape[0])
ax.set_xticks(xticks)

rows = ['$K_f$', '$K_b$', '$K_m$', '$k_{cat}$', '$K_m$', '$k_{cat}$']
ax.set_xticklabels(rows,minor=False, fontsize=fontsize,rotation=0)

colors = ['k', 'k', 'green', 'green', 'purple', 'purple' ]
for xtick, color in zip(ax.get_xticklabels(), colors):
    xtick.set_color(color)
    
ax.set_yscale('log')

yticks= np.logspace(-3,3,7 ,base=10)
ax.set_yticks(yticks, minor=False)
columns = [str(ylab) for ylab in yticks]
ax.set_yticklabels(columns,minor=False, fontsize=fontsize)
 
plt.ylabel('Reaction Rates', fontsize=fontsize)

simpleaxis(ax)
fig.set_figheight(5)
fig.set_figwidth(5)

plt.show()

4. Simulate the model and visualize bistability deterministically and stochastically

4.1 Deterministic simulation with random external perturbations

Here we pick one set of rates that we found to be bistable and assign it to our reaction network. Then we simulate the model deterministically over time and give it a kick by exchanging molecules between reactants $a$ and $b$. Note that we can only do this because this is valid according to this model's stoichiometry due to reaction $a \leftrightarrow b$. Black trace is concentration of $a$.

In [32]:
bistableRates = rateMat.T[np.where(np.array(isBistable)==1)]
In [33]:
print(np.array(allStables)[np.where(np.array(isBistable)==1)])

[list([array([2.34265752e-02, 2.07211650e+00, 3.04353028e-02, 1.21367580e-03,
       2.64386324e-01]), array([2.40812812e+00, 4.11642374e-04, 6.21518871e-04, 2.54582799e-01,
       1.10172006e-02])])
 list([array([2.98722725e-01, 1.74263246e+00, 5.70829242e-02, 3.21030098e-04,
       2.65278970e-01]), array([2.30677221e+00, 1.53112743e-03, 3.87300627e-04, 1.53877934e-01,
       1.11722066e-01])])
 list([array([5.11124903e-01, 1.54336796e+00, 5.04688674e-02, 2.30592984e-04,
       2.65369407e-01]), array([2.41962910e+00, 5.89910810e-06, 9.13192209e-07, 2.64436829e-01,
       1.16317104e-03])])
 list([array([0.01733004, 1.23291343, 0.45336669, 0.00177686, 0.26382314]), array([2.41036453e+00, 7.73112866e-05, 3.95405769e-03, 2.63149960e-01,
       2.45003978e-03])])
 list([array([2.38700351e-02, 7.20741100e-01, 7.05502190e-01, 4.15514550e-04,
       2.65184485e-01]), array([2.42034059e+00, 1.05739274e-06, 1.04949126e-04, 2.65351549e-01,
       2.48450879e-04])])]
In [34]:
bistableIndex = 1 # Chosing the first bistable rate set.
In [35]:
simdt = 1e-3
plotDt = 5e-2
runtime = 50
In [36]:
bistableRates  = np.array(bistableRates[bistableIndex])[0]
AabX.Kf, AabX.Kb, DabX.Km, DabX.kcat, Jbca.Km, Jbca.kcat = bistableRates

DabX.Km*=microMolarScaling 
Jbca.Km*=microMolarScaling
In [37]:
def setupDetSolver(kineticsBasePath = '/model/kinetics', simdt = simdt, plotDt=plotDt):
    
    ksolve = moose.Ksolve( kineticsBasePath + '/ksolve' )
    stoich = moose.Stoich(kineticsBasePath + '/stoich' )
    ksolve.numAllVoxels= 1
    stoich = moose.Stoich( kineticsBasePath +'/stoich' )
    stoich.compartment = moose.element(kineticsBasePath)
    stoich.ksolve = ksolve
    stoich.path =kineticsBasePath + "/##"
    state = moose.SteadyState( kineticsBasePath +'/state' )
   
    state.stoich = stoich
    state.convergenceCriterion = 1e-6
    
    #### Set clocks here
    moose.setClock(4, float(simdt))
    moose.useClock(4, kineticsBasePath + "/##", "process")
    moose.setClock(5, float(simdt))
    moose.useClock(5, kineticsBasePath +  '/ksolve', 'process' )
    moose.useClock(8, '/model/graphs/#', 'process' )
    moose.setClock(8, float(plotDt))

    table = {}
    
    moose.reinit()

    for species in moose.wildcardFind(kineticsBasePath+ '/##[ISA=PoolBase]'):
        tableName = '/model/graphs/plot'+ species.name
        if not moose.exists(tableName):
            table[species] = moose.Table(tableName)
            moose.connect(table[species], 'requestOut', species, 'getConc')
            moose.setClock(table[species].tick, float(plotDt))
        else:
            table[species] = moose.element(tableName)
            moose.connect(table[species], 'requestOut', species, 'getConc')
            moose.setClock(table[species].tick, float(plotDt))
    
#     matrixTable = moose.Table2("/model/graphs/matrices")
#     moose.connect(matrixTable, 'requestOut', state, 'showMatrices')
    
    moose.reinit()
    return ksolve, state
In [64]:
def plotTimeCourse(alist, blist, plotDt=plotDt):
    fontsize=12
    sumSpc = 0
    for species in moose.wildcardFind(kineticsBasePath+ '/##[ISA=PoolBase]'):
        sumSpc+=species.concInit
    ncols = len(alist)
    fig, ax = plt.subplots(figsize=(5*ncols,5), ncols=ncols)    
    for iteration in range(len(alist)):
        
        for a,b in zip(alist[iteration], blist[iteration]):
            ax[iteration].plot(np.arange(len(a))*plotDt, a, 'k', linewidth=1)
#             ax.plot(np.arange(len(b))*plotDt, b, 'gray', linewidth=1)
        ax[iteration].tick_params(axis='both', which='major', labelsize=fontsize)
        ax[iteration].tick_params(axis='both', which='minor', labelsize=fontsize)
        ax[iteration].set_xlabel("Time (s)", fontsize=fontsize)
        ax[iteration].set_ylabel("Conc. $a$ ($\mu$M)", fontsize=fontsize)
        ax[iteration].set_ylim((0,sumSpc/microMolarScaling))
    simpleaxis(ax)
    return plt, ax
In [39]:
deleteSetup()
ksolve, state = setupDetSolver()
plota = moose.element("/model/graphs/plota")
plotb = moose.element("/model/graphs/plotb")
plotc = moose.element("/model/graphs/plotc")
In [40]:
alist, blist, clist = {}, {}, {}
frac = [0.05, 0.95] ## Swapping ratios to perturb the system with
numIterations = len(frac)

a = moose.element("/model/kinetics/a")
b = moose.element("/model/kinetics/b")
c = moose.element("/model/kinetics/c")
In [41]:
a.conc, b.conc
Out[41]:
(0.002357000000000002, 6.379999999999999e-05)
In [52]:
for iteration in range(numIterations):     
    alist[iteration] = []
    blist[iteration] = []
    clist[iteration] = []

    moose.start(float(runtime))
    
    ## Swapping molecules between a and b
    kickConc = frac[iteration] * a.conc

    a.conc = a.conc - kickConc
    b.conc = b.conc + kickConc
    moose.start(float(runtime))
    
    ## Exchanging back molecules between a and b
    
    kickConc = frac[iteration] * b.conc
    a.conc = a.conc + kickConc
    b.conc = b.conc - kickConc
    moose.start(float(runtime))

    alist[iteration].append(plota.vector[2:]/microMolarScaling)
    blist[iteration].append(plotb.vector[2:]/microMolarScaling)
    clist[iteration].append(plotc.vector[2:]/microMolarScaling)
    
    moose.reinit()

In the 5% perturbation case, both attempts fail to lead to a transition. With 95% perturbation, the first attempt leads to a transition, but the second attempt with the swapping back of molecules fails.

In [71]:
plt, ax = plotTimeCourse(alist, blist, plotDt=plotDt)
ax[0].text(x=100, y = 2.5, s="1, 5% $a$", color='r', fontsize=fontsize)
ax[0].text(x=200, y = 2.5, s="2, 5% $b$", color='r', fontsize=fontsize)
ax[1].text(x=100, y = 2.5, s="1, 95% $a$", color='r', fontsize=fontsize)
ax[1].text(x=200, y = 2.5, s="2, 95% $b$", color='r', fontsize=fontsize)
plt.show()

4.2 Stochastic simulation (internal fluctations)

Bistable behavior of the model that we found can be seen using stochastic simulation, where the concentration vectors show spontaneous transitions between two stable-states. Simulations were done at 0.008 fL for 300 seconds. Black trace is concentration of molecule $a$.

In [72]:
runtime = 300
vol = 8e-21
numIterations = 5
In [73]:
def setupStochSolver(kineticsBasePath = '/model/kinetics', simdt = simdt, plotDt=plotDt):
    
    ksolve = moose.Ksolve( kineticsBasePath + '/ksolve' )
    gsolve = moose.Gsolve(kineticsBasePath + '/gsolve')
    stoich = moose.Stoich(kineticsBasePath + '/stoich' )
    
    stoich = moose.Stoich( kineticsBasePath +'/stoich' )
    stoich.compartment = moose.element(kineticsBasePath)
    state = moose.SteadyState( kineticsBasePath +'/state' )
    
    gsolve.numAllVoxels= 1
    stoich.compartment = moose.element(kineticsBasePath )
    stoich.ksolve = gsolve
    stoich.path =kineticsBasePath + "/##"
   
    state.stoich = stoich
    state.convergenceCriterion = 1e-6
    
    #### Set clocks here
    moose.setClock(4, float(simdt))
    moose.useClock(4, kineticsBasePath + "/##", "process")
    moose.setClock(5, float(simdt))
    moose.useClock(5, kineticsBasePath +  '/gsolve', 'process' )
    moose.useClock(8, '/model/graphs/#', 'process' )
    moose.setClock(8, float(plotDt))

    table = {}
    
    moose.reinit()

    for species in moose.wildcardFind(kineticsBasePath+ '/##[ISA=PoolBase]'):
        tableName = '/model/graphs/plot'+ species.name
        if not moose.exists(tableName):
            table[species] = moose.Table(tableName)
            moose.connect(table[species], 'requestOut', species, 'getConc')
            moose.setClock(table[species].tick, float(plotDt))
        else:
            table[species] = moose.element(tableName)
            moose.connect(table[species], 'requestOut', species, 'getConc')
            moose.setClock(table[species].tick, float(plotDt))
    
    moose.reinit()
    return gsolve, state
In [74]:
deleteSetup()
gsolve, state = setupStochSolver()
moose.element("/model/kinetics/").volume = vol #m^3 = 1000L
In [75]:
alist, blist, clist = {}, {}, {}

for iteration in range(numIterations):
    alist[iteration] = []
    blist[iteration] = []
    clist[iteration] = []
    
    state.randomInit()

    moose.start(runtime)

    a = plota.vector[1:]/microMolarScaling
    b = plotb.vector[1:]/microMolarScaling
    c = plotc.vector[1:]/microMolarScaling
    moose.reinit()

    alist[iteration].append(a)
    blist[iteration].append(b)
    clist[iteration].append(c)

Spontaneous transitions of $a$ between a high and a low state can be seen in the figure below.

In [76]:
plt, ax = plotTimeCourse(alist, blist, plotDt=plotDt)
plt.show()